Skip to main content

Multivariate analysis based on partial least squares regression

Multivariate analysis (MVA) is based on the statistical principle of multivariate statistics, which involves observation and analysis of more than one statistical outcome variable at a time.

Partial least squares regression (PLS regression) is a particular type of MVA. PLS provides quantitative multivariate modelling methods, with inferential possibilities similar to multiple regression, t-tests and ANOVA. It constructs linear model using latent factors that

  • maximally summarize the variation of the predictors
  • maximize correlation with the response variable.

Regress and analyze​

  1. Open a table.
  2. On the Top Menu, select ML | Analyze | Multivariate Analysis.... A dialog opens.
  3. In the dialog, specify
    • the column with responce variable (in the Predict field)
    • the columns with the predictors (in the Using field)
    • the number of Components, i.e. latent factors
    • Names of data samples
  4. Press Run to execute. You get
    • the Observed vs. Predicted scatterplot comparing the responce to its prediction
    • the Regression Coefficients bar chart presenting parameters of the obtained linear model
    • the Loadings scatterplot indicating the impact of each feature on the latent factors
    • the Scores scatterplot reflecting data samples similarities and dissimilarities
    • the Explained Variance bar chart measuring how well the latent factors fit source data

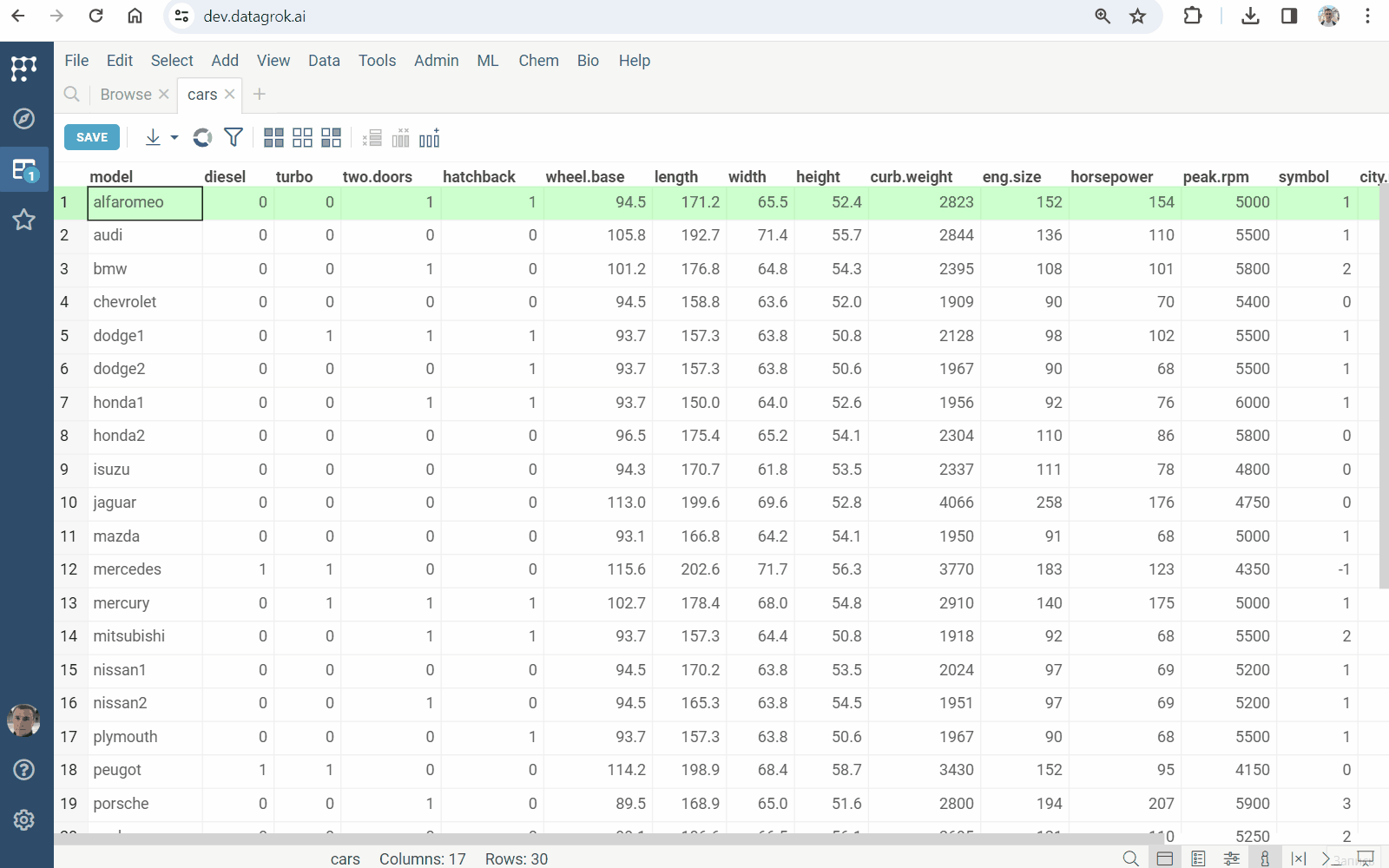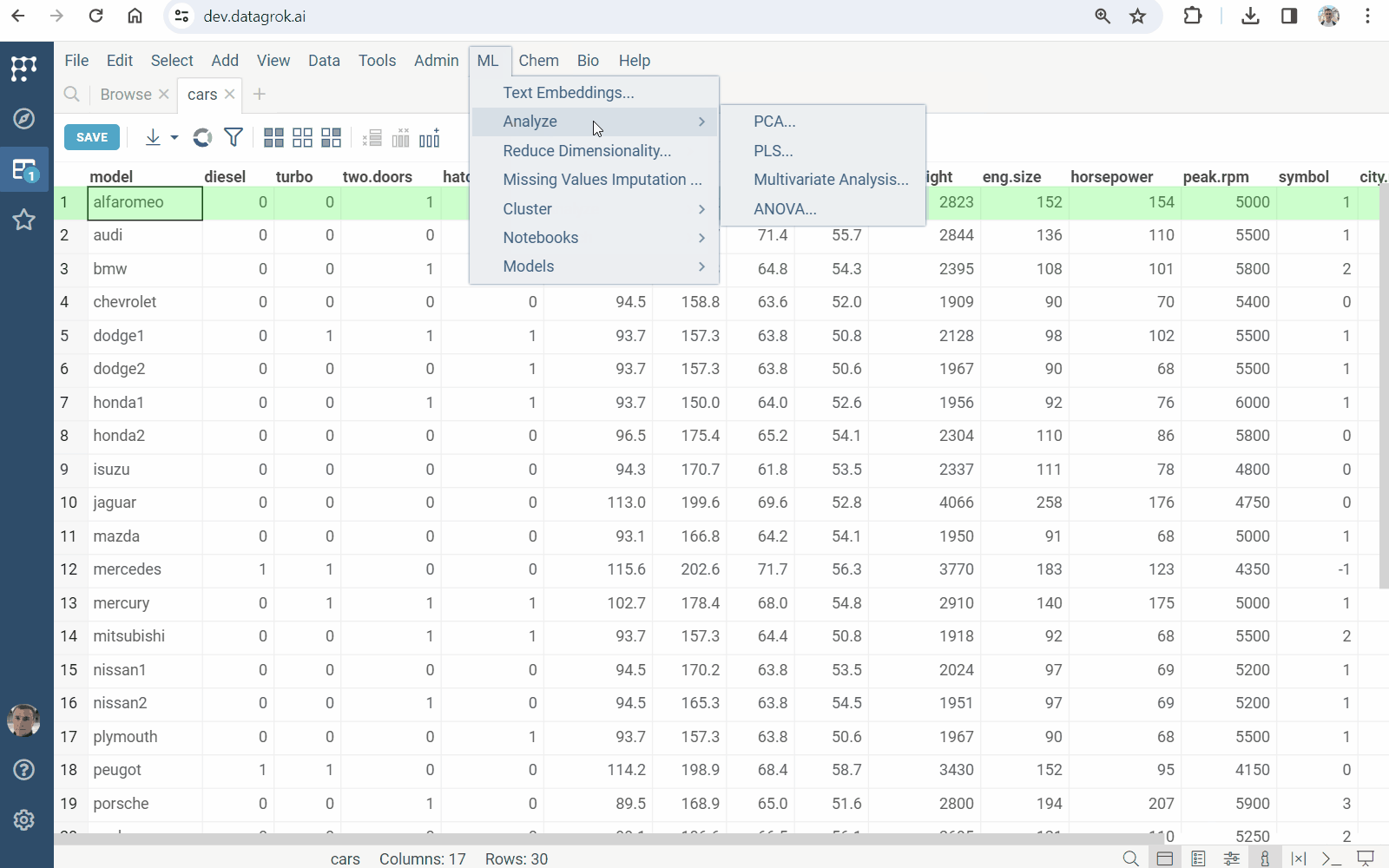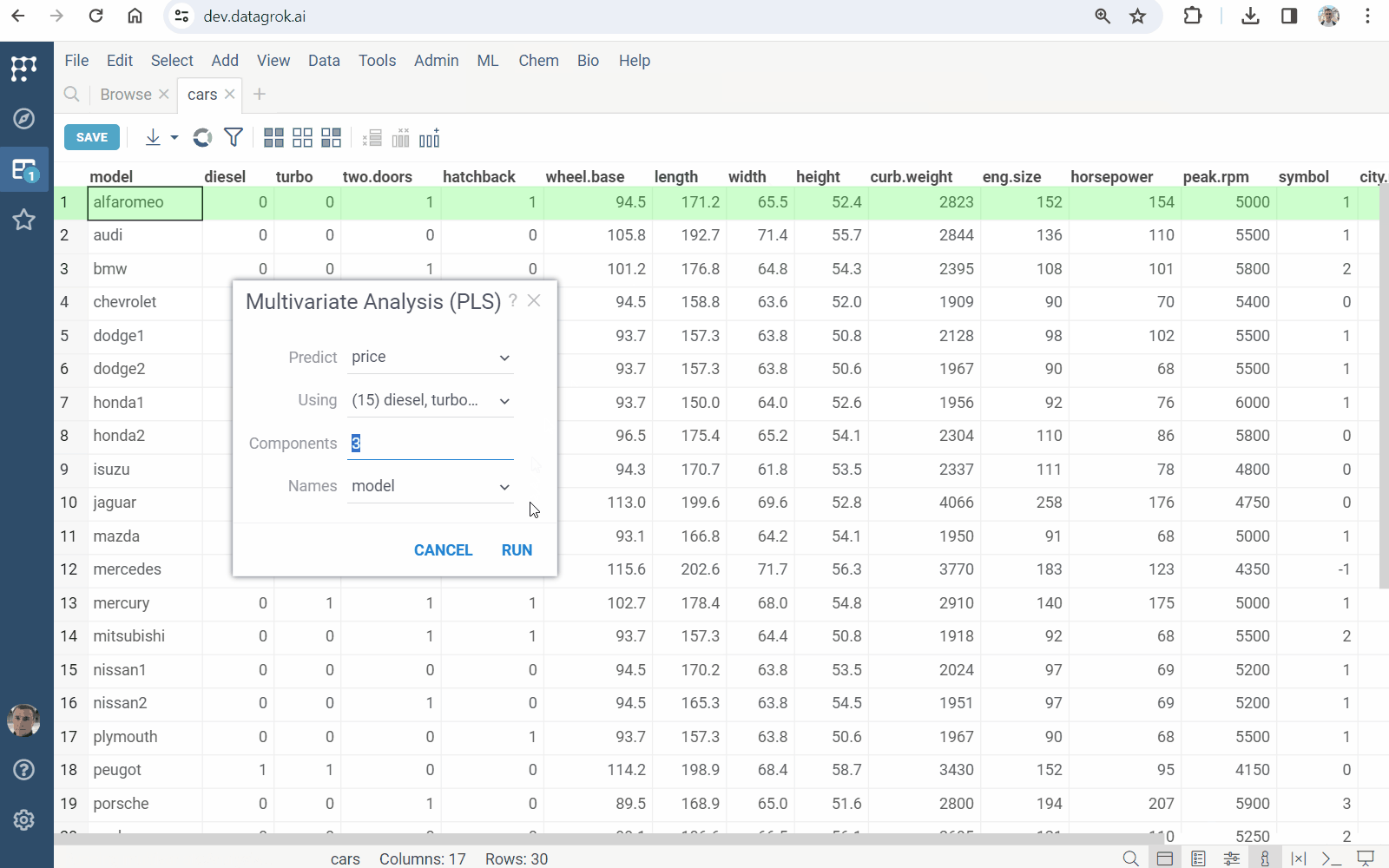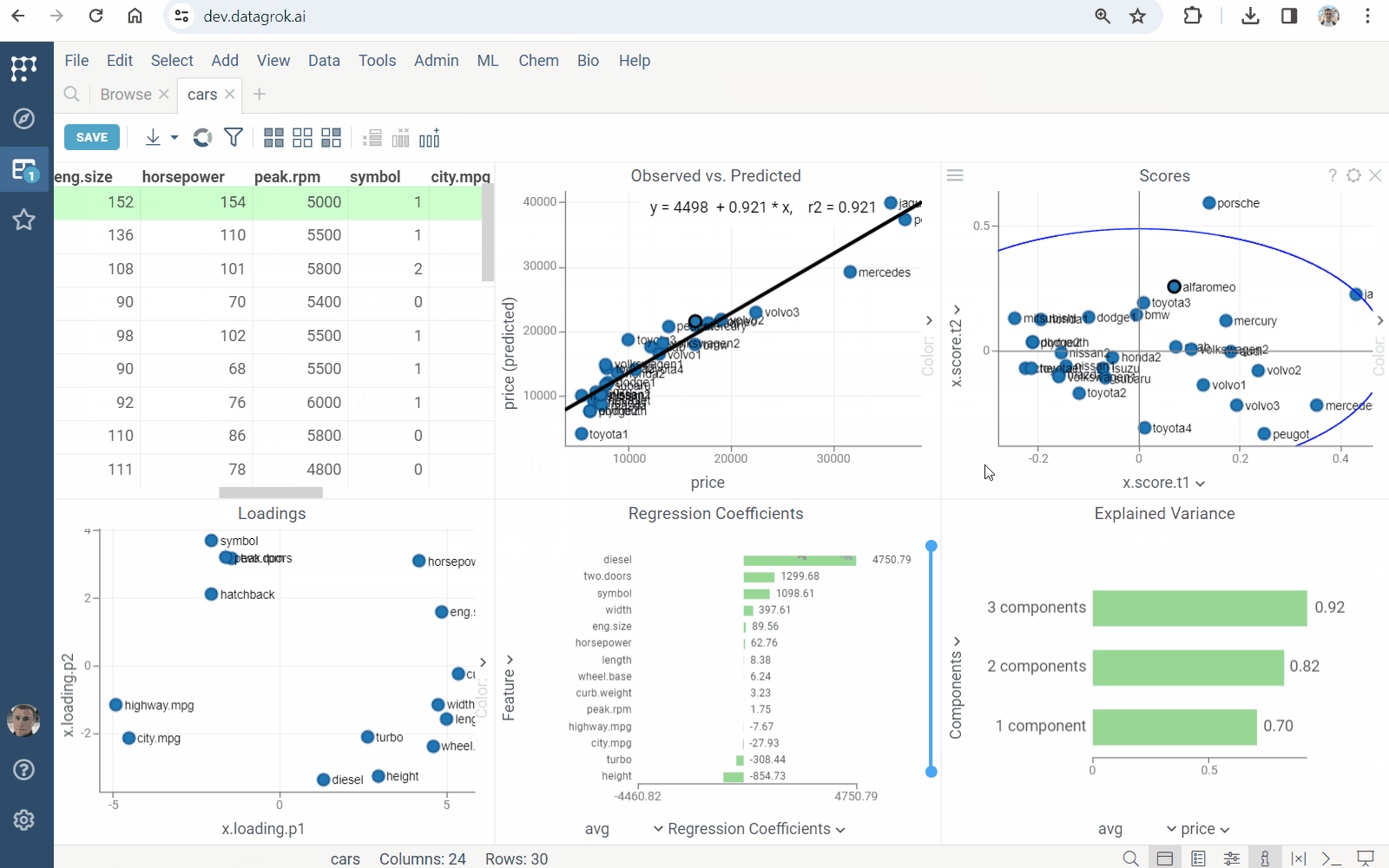
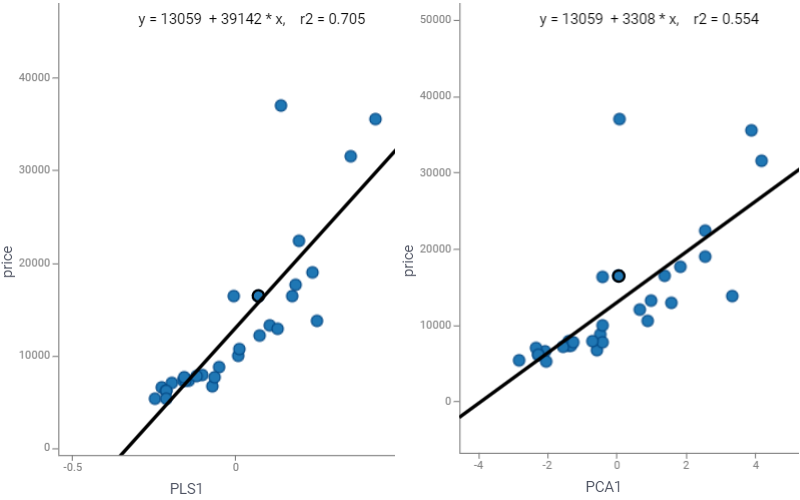
add-to-workspace

PLS components​

Compute the predictors representation by the latent factors:

  1. Open a table.
  2. On the Top Menu, select ML | Analyze | PLS.... A dialog opens.
  3. In the dialog, specify
    • the column with responce variable (in the Predict field)
    • the columns with the predictors (in the Using field)
    • the number of Components, i.e. latent factors

PLS components contain more predictive information than ones provided by principal component analysis (PCA). The coefficient of determination r2 indicates this:

add-to-workspace

See also​