Sequence Space
Sequence space performs dimensionality reduction on a column of biological sequences.
Dimensionality reduction can be used to visualize high-dimensional data in two dimensions. It is particularly useful for visualizing the clusters of similar sequences on 2D scatter plot. The algorythm uses either UMAP or t-SNE, in combination with sequence distance functions, to calculate the distances between sequences and then reduce the dimensionality of the data.
Usage
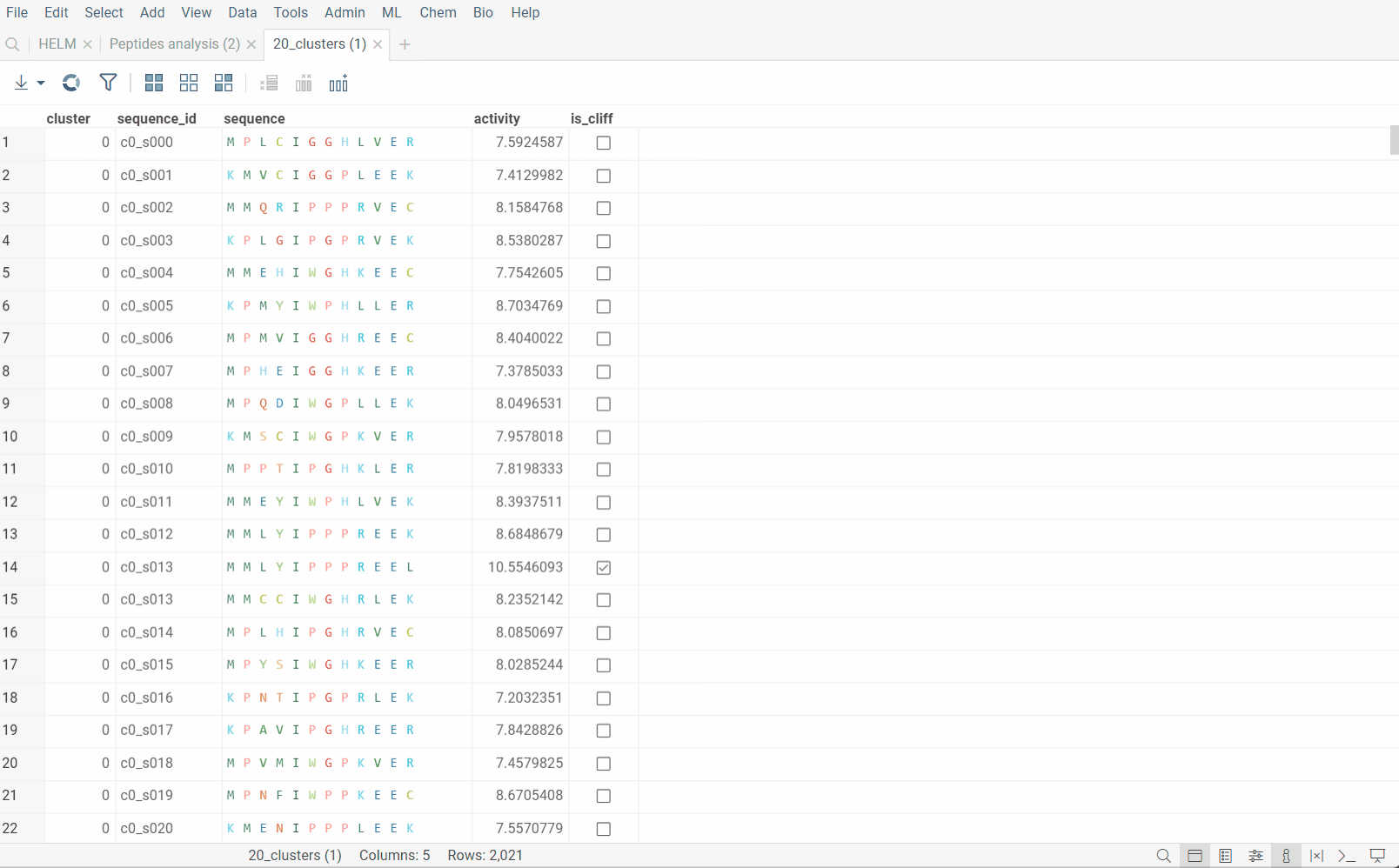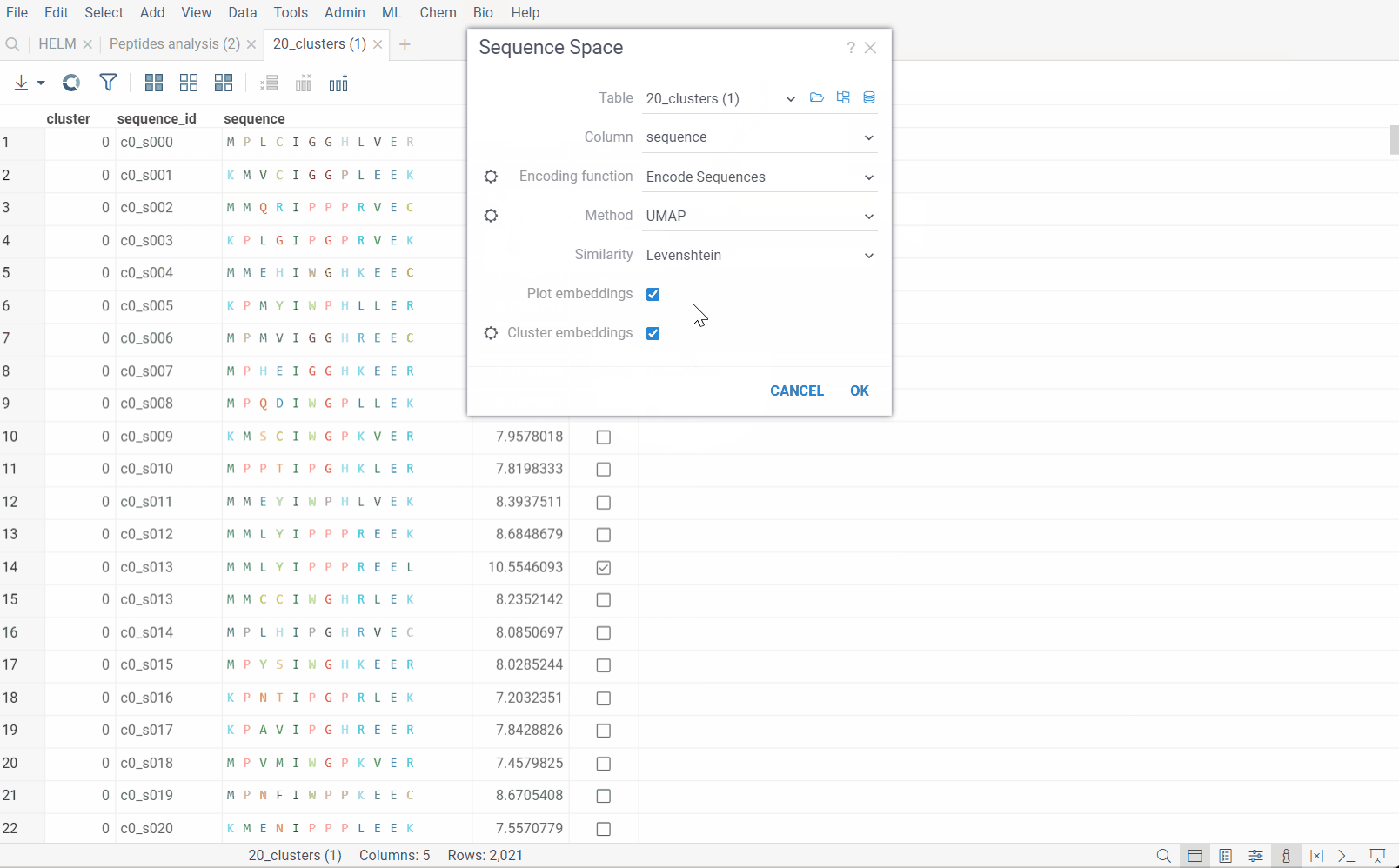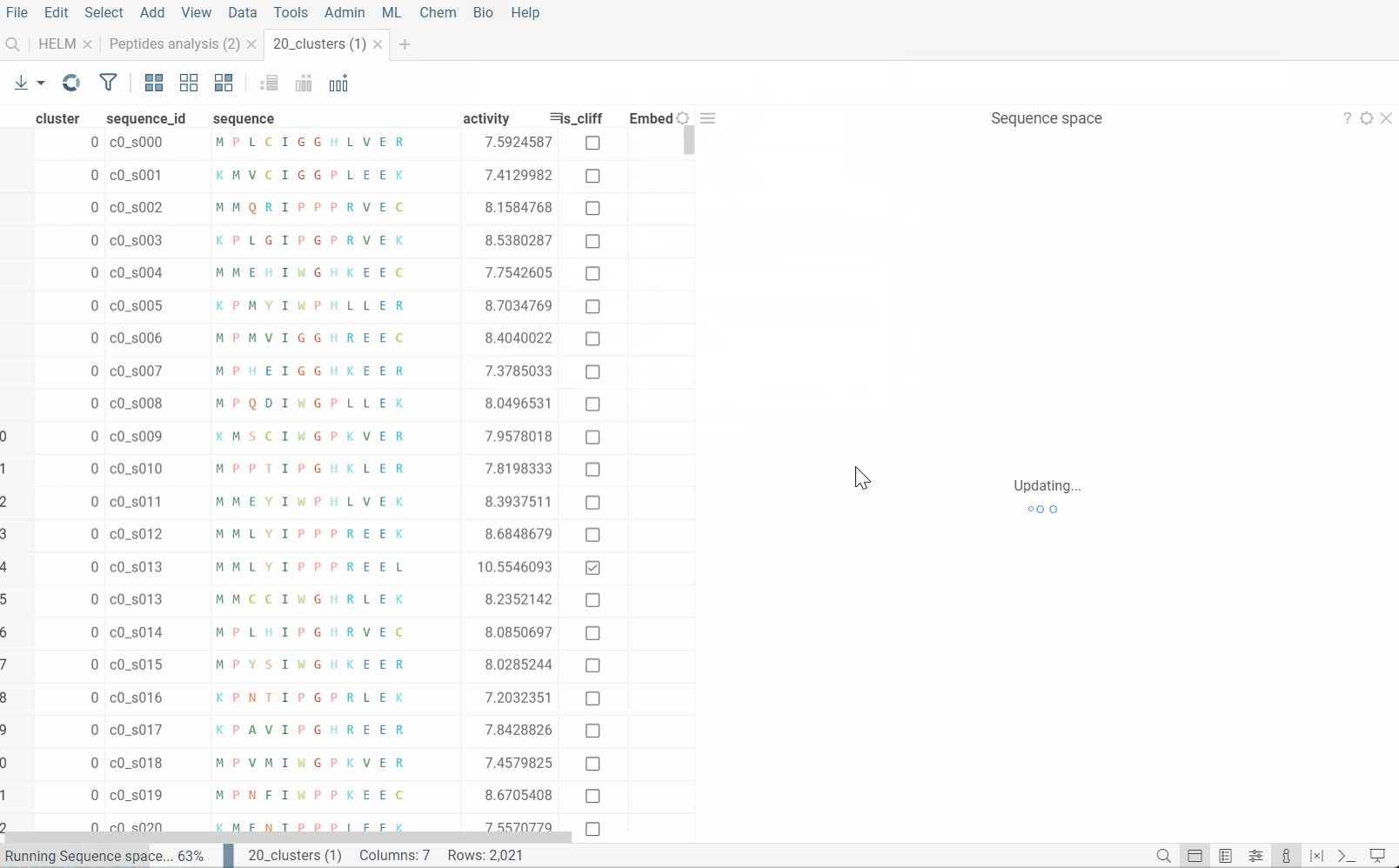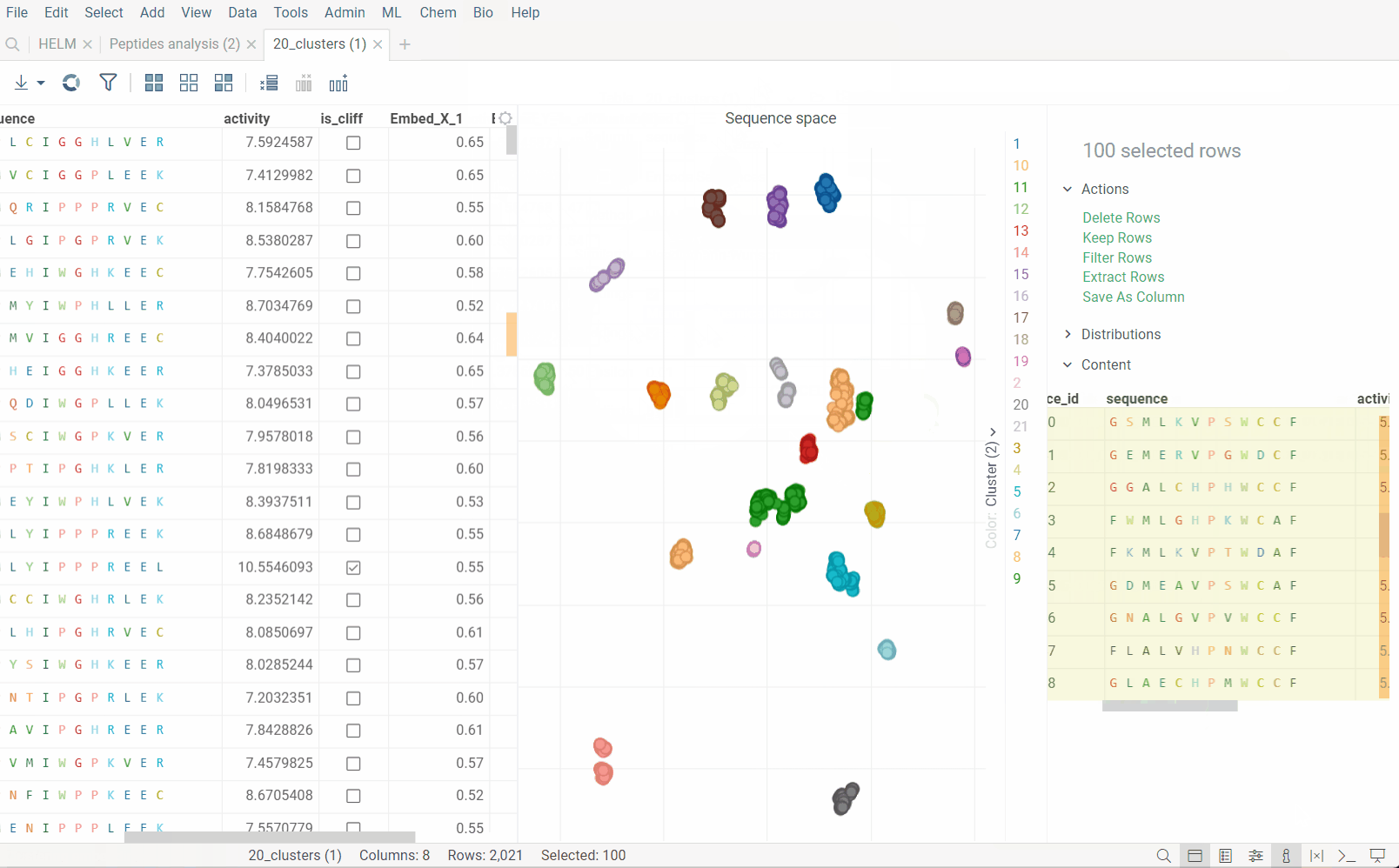
The dialog has the following inputs:
Table: The table containing the column of sequences.
Column: The column containing the sequences.
Encoding function: The encoding function that will be used for pre-processing of sequences. For non-helm notation sequences, only one encoding function is available, that will encode them in single charachter form and calculate the substitution matrix for each individual monomer. For Helm sequences, apart from prior function, another one is offered that will use chemical fingerprint distances between each macromolecule to calculate distance matrix. The
Encode sequencesfunction has 3 parameter which you can adjust using the gear (⚙️) button next to the encoding function selection:- Gap open penalty: The penalty for opening a gap in the alignment (used for Needleman-Wunsch algorythm).
- Gap extend penalty: The penalty for extending a gap in the alignment (used for Needleman-Wunsch algorythm).
- Fingerprint type: The type of molecular fingerprints that will be used to generate monomer substitution matrix.
Method: The dimensionality reduction method that will be used. The options are:
UMAP: UMAP is a dimensionality reduction technique that can be used for visualisation similarly to t-SNE, but also for general non-linear dimension reduction.
t-SNE: t-SNE is a machine learning algorithm for dimensionality reduction developed by Geoffrey Hinton and Laurens van der Maaten. It is a nonlinear dimensionality reduction technique that is particularly well-suited for embedding high-dimensional data into a space of two or three dimensions, which can then be visualized in a scatter plot.
Other parameters for dimensionality reduction method can be accessed through the gear (⚙️) button next to the method selection.
Similarity: The similarity/distance function that will be used to calculate pairwise distances. The options are:
- Needleman-Wunsch: Needleman-Wunsch is a dynamic programming algorithm that performs a global alignment on two sequences. It is commonly used in bioinformatics to align protein or nucleotide sequences.
- Hamming: Hamming distance is a metric for comparing two macromolecules of same length. Hamming distance is the number of positions in which the two monomers are different.
- Monomer chemical distance: Similar to Hamming distance, but instead of penalizing the missmatch of monomers with -1, the penalty will be based on the chemical distance between the two monomers. The chemical distance is calculated using the chemical fingerprint of the monomers.
- Levenshtein: Levenshtein distance is a string metric for measuring the difference between two sequences. Informally, the Levenshtein distance between two sequences is the minimum number of single-monomer edits (insertions, deletions or substitutions) required to change one sequence into the other.
Plot embeddings: If checked, the plot of the embeddings will be shown after the calculation is finished.
Cluster embeddings: If checked, the embeddings will be clustered using the DBSCAN algorithm. The DBSCAN algorithm groups together points that are closely packed together (points with many nearby neighbors), marking as outliers points that lie alone in low-density regions (whose nearest neighbors are too far away). The DBSCAN algorithm has two parameters that you can adjust through the gear (⚙️) button next to the cluster embeddings checkbox:
- Epsilon: The maximum distance between two points for them to be considered as in the same neighborhood.
- Minimum points: The number of samples (or total weight) in a neighborhood for a point to be considered as a core point. This includes the point itself.